This algorithm uses a standard deck of cards with 52 suited cards and two jokers which are distinguishable from each other, called the A joker and the B joker. For simplicity’s sake, only two suits will be used in this example, clubs and diamonds. Each card is assigned a numerical value: the clubs will be numbered from 1 to 13 (Ace through King) and the diamonds will be numbered 14 through 26 in the same manner. The jokers will be assigned the values of 27 and 28. Thus, the jack of clubs would have the value 11, and the deuce of diamonds would have the value 15. (In a full deck of cards, the suits are valued in bridge order: clubs, diamonds, hearts, spades, with the suited cards numbered 1 through 52, and the jokers numbered 53 and 54.)
To begin encryption or decryption, arrange the deck of cards face-up in an order previously agreed upon. The person decrypting a message must have a deck arranged in the same order as the deck used by the person who encrypted the message. How the order is initially decided upon is up to the recipients; shuffling the deck perfectly randomly is preferable, although there are many other methods.
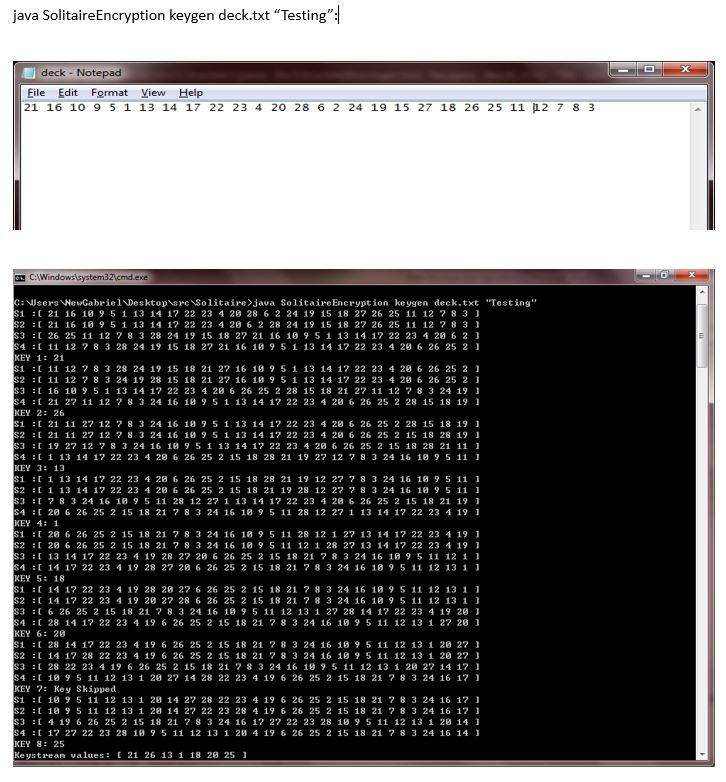
The algorithm generates a keystream, a sequence of values which are combined with the message to encrypt and decrypt it. Each value of the keystream is used to encrypt one character of the message, so the keystream must be at least as long as the message. If the keystream is longer than the message the message may be padded with an additional repeated character, thus denying the attacker knowledge of the exact length of the message.
To encrypt a message:
- Remove all punctuation and spaces, leaving only the 26 letters A–Z.
- Convert each letter to its natural numerical value, A = 1, B = 2, …, Z = 26.
- Generate one keystream value for each letter in the message using the keystream algorithm below.
- Add each keystream value to the corresponding plaintext number, subtracting 26 if the resulting value is greater than 26. (In mathematics this is called modular arithmetic.)
- Convert the resulting numbers back to letters. This sequence of letters is the ciphertext.
To decrypt a ciphertext:
- Convert each letter in the ciphertext to its natural numerical value.
- Generate one keystream value for each letter in the ciphertext.
- Subtract each keystream value from the corresponding ciphertext value, adding 26 if the resulting value is less than 1.
- Convert the resulting numbers back to letters.
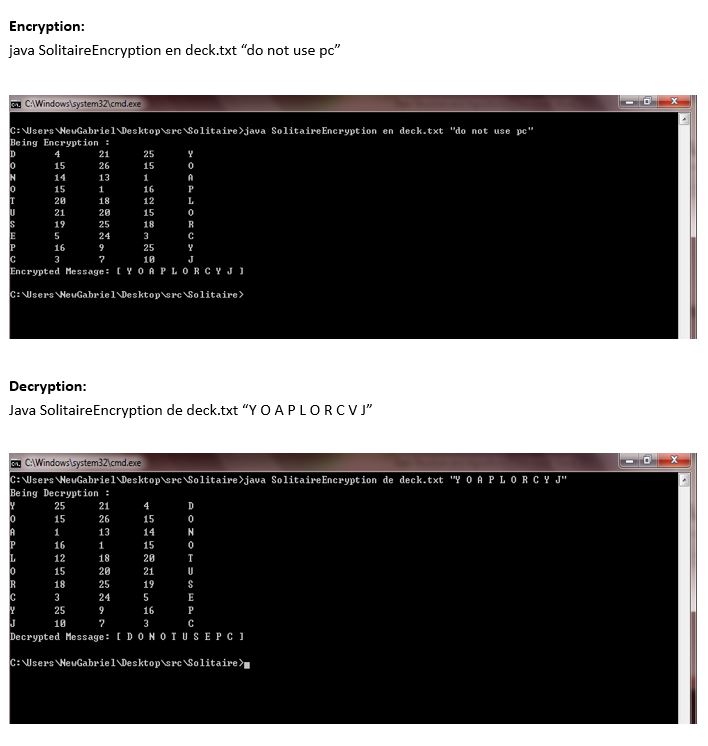
Let’ s try on it
| Plaintext | D | O | N | O | T | U | S | E | P | C |
| (number representation) | 4 | 15 | 14 | 15 | 20 | 21 | 19 | 5 | 16 | 3 |
| Keystream values | 21 | 6 | 13 | 1 | 18 | 20 | 25 | 24 | 9 | 7 |
| (encoded numbers) | 25 | 15 | 1 | 16 | 12 | 15 | 18 | 3 | 25 | 10 |
| Ciphertext | Y | O | A | P | L | O | R | C | Y | J |